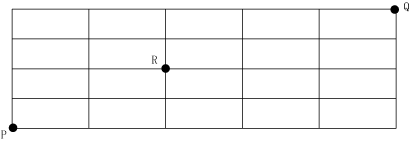
図の線上を点Pから点Rを通って, 点Qに至る最短経路は何通りあるか。
ア 16
イ 24
ウ 32
エ 60
解説を読む
正解:エ
解説:
組み合わせの問題ですが、PからR、RからQを分けて考えてみます。まずはPからQの最短ルートが何通りあるかという問題です。
PからRに移動するには水平方向(右)に2移動します。同じように垂直方向(上)にも2移動します。合計の移動距離は2+2=4となります。
すると4回移動するうちに2回は垂直方向に移動すると考えることが出来ます。
$${}_2 C_4 =\frac{4!}{2!(4-2)!}=\frac{4\times3\times2\times1}{2\times1\times2\times1}=\frac{24}{4}=6通り$$
同様にRからQに移動するには水平方向に3、垂直方向にも2移動します。合計の移動距離は3+2=5となります。
すると5回移動するうちに2回は垂直方向に移動すると考えることが出来ます。
$${}_2 C_5 =\frac{5!}{2!(5-2)!}=\frac{5\times4\times3\times2\times1}{2\times1\times3\times2\times1}=\frac{120}{12}=10通り$$
PからRが6通り、RからQが10通りの経路が存在することが分かったので$$6\times10=60通り$$経路が存在しエが正解となります。
解説を閉じる


コメント