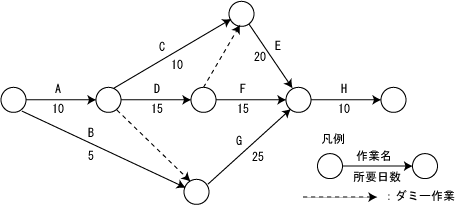
図のプロジェクトの日程計画において,プロジェクトの所要日数は何日か。
ア 40
イ 45
ウ 50
エ 55
解説を読む
正解:エ
解説:
アローダイアグラム(PERT図)の所要日数はクリティカルパス上の日数となります。クリティカルパスはすべての経路の中で待ち時間の発生しない最短経路のことです。クリティカルパスを求めるには最早結合点と最遅結合点を求め等しい値となる結合点を辿ることで求めることができます。別の方法としてはすべての経路を書き出し最も大きい値となる経路をクリティカルパスとすることもできます。
A→C→E→H => 10+10+20+10 = 50
A→D→E→H => 10+15+20+10 = 55
A→D→F→H => 10+15+15+10 = 50
A→G→H => 10+25+10 = 45
B→G→H => 5+25+10 = 40
上記の通り最も大きい値の55日が所要日数となりADEHの経路がクリティカルパスとなります。したがってエが正解です。
クリティカルパスを求める問題は頻出ですが、最も大きい値が最小の所要日数になることに対して苦手意識を持つ方が多いようです。上記の場合の最小値の経路はBGHとなりますが、Hの作業を行うためにはGからだけでなくEとFの作業も終わっている必要があります。すなわちGの作業が終わっていても待ち時間が発生してしまいます。対してクリティカルパス上にあるEの作業の場合はFとGの作業をすでに終わっているので待ち時間なくHの作業に入ることができます。すなわちクリティカルパスは最小所要日数の経路ですが言い換えると待ち時間の発生しない経路と考えることもできます。
解説を閉じる


コメント